3.4.4 Normal Vector

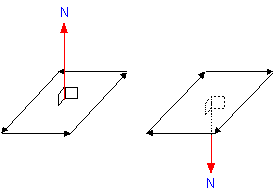
A vector that expresses the vertical direction of a surface is called a normal vector:

How to Calculate a Normal Vector

To calculate the normal vector of a surface, you need to find what is called the cross-product of the two vectors that specify that surface. You can use the following step-by-step technique to calculate the cross-product of two vectors
and where:

1. Arrange and write down the coordinates of each vector and as two lines like this:
   
   
   
   
   
2. Repeat each X coordinate of and on the far right end of each line like this:
   
   
   
   
   
3. Draw connecting lines like this:
   
   
   
   
4. Calculate , , and using these formulas:
   
   
   
   
   
   is the X coordinate of the result, is the Y coordinate, and is the Z coordinate.
   
   

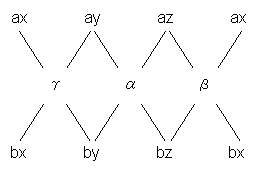
In summary, to obtain the cross-product of vectors and , use this formula:

Example Calculation

Here is a second example that shows how to find the normal vector N of the plane defined by the three points A, B and P shown in this illustration:

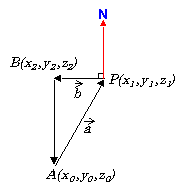
Note: When working with the two vectors and , you must be very careful to factor in each vector's direction.

Calculate the normal vector N by using this formula:

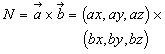
To get the cross-product of the vectors, apply these formulas:

Because and are vectors, specify each coordinate component like this:

Therefore, the final detailed formula for the normal vector N (Nx,Ny,Nz) is:

You need the cross-product for many geometric calculations, not just to calculate the normal vector.

Nintendo® Confidential

Copyright © 1999
Nintendo of America Inc. All Rights Reserved
Nintendo and N64 are registered trademarks of Nintendo

Last Updated March, 1999