N64 Programming Manual Chapter 11

Matrix State

The “geometry engine” in the RSP implements a fixed-point matrix engine with the following matrix state:

A 10-deep modeling matrix stack. New matrices can be loaded onto the stack, multiplied with the top of the stack, popped off of the stack, etc. This matrix stack is primarily used for manipulating objects within the world coordinate system (often combinations of rotations, translations, and sometimes scales).

A 1-deep projection and viewing matrix “stack”. New matrices can be loaded onto the stack, multiplied with the top of the stack, but cannot be pushed or popped. This matrix “stack” is primarily used for the projection matrix and the viewing matrix. The projection matrix (often created with the guPerspective or the guOrtho functions) is loaded onto the stack, and then the viewing matrix (often created with the guLookAt function) is multiplied on top of it.

A “perspective normalization” factor. This is used to improve precision of the fixed-point perspective computation.

When a group of vertices is loaded, they are first transformed by the matrix MP (the current top of the modeling stack multiplied by the projection matrix). All vertex transformations are done only when they are loaded; sending a new matrix down later will not change any points already in the points buffer.

The modeling matrix stack resides in DRAM. It is the application’s responsibility to allocate enough memory for this stack and provide a pointer to this stack area in the task list.

The format of a matrix is a bit unusual. It is optimized for the RSP’s vector unit (used during the multiplies and transformations.) This format groups all of the integer parts of the elements, followed by all of the fractional parts of the elements. This unusual format is not exposed to the user, unless he/she chooses not to use the matrix utilities in the libraries.

Insert a Matrix
Inserts a new matrix into the display list.

Table 1 gsSPMatrix(Mtx *m, unsigned int p)

Parameter Values

m pointer to the new matrix

p G_MTX_MODELVIEW or G_MTX_PROJECTION,
G_MTX_MUL or G_MTX_LOAD,
G_MTX_PUSH or G_MTX_NOPUSH

Pop a Matrix
This command pops the matrix stack.

Table 2 gsSPPopMatrix(unsigned int n)

Parameter Values

n unused

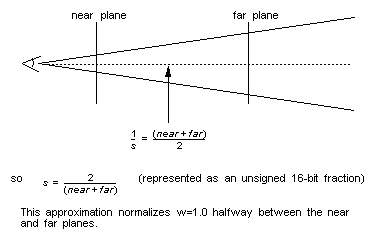
Perspective Normalization
This scale value is used to scale the transformed w coordinate down, prior to dividing out w to compute the screen coordinates (which are similarly scaled). The effect of this is to maximize the precision of this divide.

The library function guPerspective( ) returns one approximation for this scale value, which is a good estimate for most cases:

Figure 11.3.1 Perspective Normalization Calculation

Table 3 gsSPPerspNormalize(unsigned short int s)

Parameter Values

s 16-bit unsigned fractional perspective normalization scale

Note on Coordinate Systems and Big Numbers
The RSP is a fixed point machine, so keeping coordinate systems within a certain range is important. If numbers in the final coordinate system (or intermediate coordinate systems) are too big, then the geometry of objects can be distorted, textures can shift erratically, and clipping can fail to work correctly. In order to avoid these problems keep the following notes in mind:

No coordinate componant (x, y, z, or w) should ever be greater than 32767.0 or less than -32767.0
The difference between any 2 vertices of a triangle should not have any componants greater than 32767.0
The sum of the difference of w’s of any 2 vertices plus the sum of the differneces of any of the x, y, or z componants should be less than 32767.0. In other words for any 2 vertices in a triangle, v1=(x1,y1,z1,w1), and v2=(x2,y2,z2,w2), these should all be true:

              abs(x1-x2) + abs(w1-w2) < 32767.0
              abs(y1-y2) + abs(w1-w2) < 32767.0
              abs(z1-z2) + abs(w1-w2) < 32767.0

One way to check this is to take the largest vertices that you have and run them throught the largest matrices you are likely to have, then check to make sure that these conditions are met.

A reccommended way of avoiding trouble is to never allow any componant to get larger than 16383.0 or smaller than -16383.0. To ensure this find:

M = the largest componant (x, y, or z) of the largest model in your database.
S = The largest scale (ie number in the upper 3 rows of the matrix) in the matrix made up of the concatenation of the largest modeling matrix, the largest LookAt matrix, and the largest Perspective matrix you will use.
T = the largest translation (ie number in the 4th row of the matrix) in the matrix made up of the concatenation of the largest modeling matrix, the largest LookAt matrix, and the largest Perspective matrix you will use.

Now M * S + T < 16383.0 should be true. If you experience textures wobbling or shifting over a surface, clipping not working correctly, or geometry behaving erratically, this is a good place to check.

A Few Words About Matrix Precision
The RSP uses fixed-point 32-bit multiplies during matrix operations. Since the product of two 32-bit numbers is a 64-bit number, only the middle 32 bits of the answer is retained. Overflow of intermediate terms is possible, especially in large coordinate systems or unusual projection matrices.

In order to avoid fixed-point precision problems, in some cases it may be desirable to compute the matrix in floating point on the R4300 and just load it.

Matrix multiplies are very fast on the RSP, but they are not free. If possible, reduce matrix operations by pre-multiplying the matrices at modeling time or compile time.

Parameter	Values
m	pointer to the new matrix
p	G_MTX_MODELVIEW or G_MTX_PROJECTION, G_MTX_MUL or G_MTX_LOAD, G_MTX_PUSH or G_MTX_NOPUSH

Parameter	Values
s	16-bit unsigned fractional perspective normalization scale