1-5 Matrix Specification


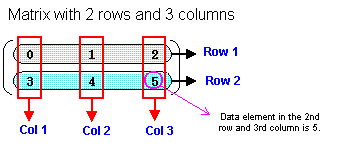
A matrix is made up of rows and columns. Rows are numbered from top to bottom, and columns are numbered from left to right. A matrix that has m rows and n columns is called a matrix of m rows and n columns or an, m x n ,matrix. An individual cell in a matrix is called an element or component and is referenced as the element in row m and column n or as the (m, n) component.

Figure 1-5-1 Matrix


You will usually use 4 x 4 matrices in 3D graphics and 3 x 3 matrices in 2D graphics. These matrices are specified like this:

or



1-5-1 Matrix Addition and Subtraction


Adding or subtracting matrices is accomplished by using this formula:



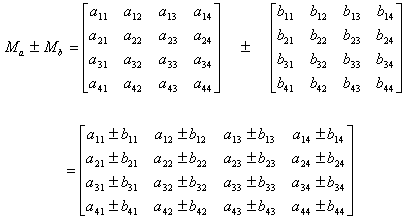
Here's an easy example showing how to add matrices together:



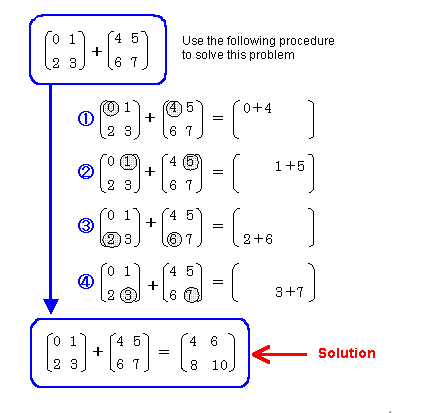
Figure 1-5-2 Matrix Addition 1


Here's another example. This one switches the order of the same matrices and shows that the result is still the same:



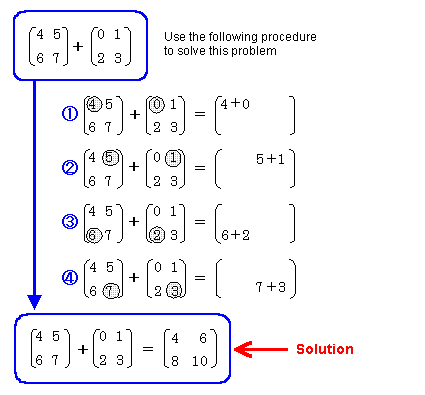
Figure 1-5-3 Matrix Addition 2


As you can see from these examples, the commutative law is valid for matrix addition and subtraction. In other words, you can switch the calculation order:

(The commutative law is valid)
(The associative law is valid)



1-5-2 Matrix Multiplication


When you multiply one matrix by another matrix, the result is also a matrix. This section explains the calculation method for Matrix Multiplication.

If you multiply matrix by matrix , the result is . Use the following formula to obtain each element of row i and column j in the resulting matrix where :



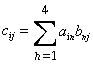
For example, to calculate the element in the second row and third column of , use this formula:



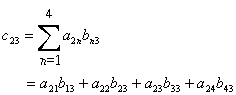
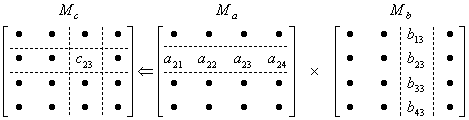
As you can see, the element of the second row and the third column is the product-sum of the second row of the matrix and third column of the matrix as illustrated here:



Note that for matrix multiplication to be possible, the number of columns in matrix A (m rows n columns) must equal the number of rows in matrix B (p rows q columns). In other words, n and p in the following illustration must be equal:



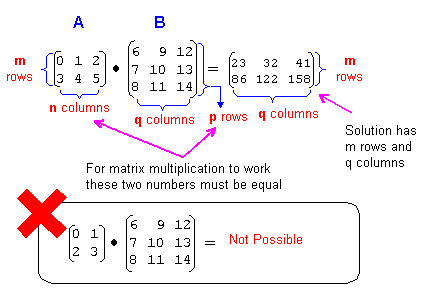
Figure 1-5-4 The criteria for matrix multiplication


Next, an additional example of multiplication will be provided using a simpler matrix.



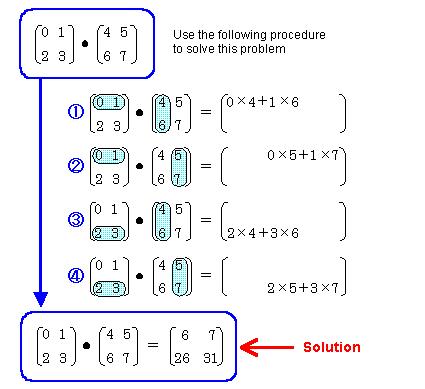
The following is another example which shows how the results differ when the order of the matrix multiplication is changed:



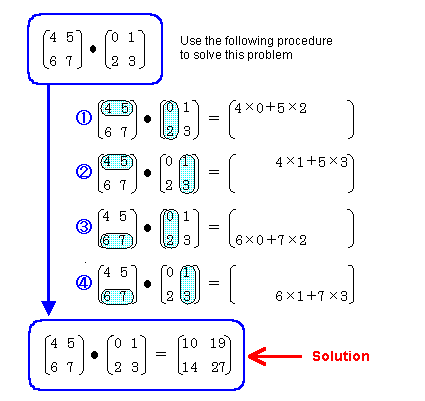
Figure 1-5-5 Matrix Multiplication


Matrix Multiplication. However, the associative law is valid for matrix multiplication.

(the commutative law is invalid)
(the associative law is valid)