gSPMatrix

#include <ultra64.h> /* gbi.h */
gSPMatrix(Gfx *gdl, Mtx *matrix, u8 param)
gsSPMatrix(Mtx *matrix, u8 param)

Arguments

• gdl is the display list pointer.

• matrix is the 4x4 fixed-point matrix.

• param is the operation flags:
  (* Multiple flags can be specified as the bit sum of the flags.)
  G_MTX_PROJECTION (Operate on the projection matrix stack)
  G_MTX_MODELVIEW (Operate on the model view matrix stack)
  G_MTX_MUL (Multiply top of matrix stack and matrix m)
  G_MTX_LOAD (Load matrix m at top)
  G_MTX_NOPUSH (Do not push on matrix stack before matrix operation)
  G_MTX_PUSH (Push on matrix stack before matrix operation)

Explanation
gSPMatrix inserts matrix operations in the display list. With these argument specifications you can set which matrix stack to use (projection or model view), the loading position, and whether to concatenate or push. For details, please see Section 11.3, "Matrix State" in the N64 Online Programming Manual.

• Concerning the matrix argument:
  This format is hidden in the graphics utility library and is usually not revealed to the programmer. However, it is necessary to understand this format in certain cases (static matrix declarations or direct operation on elements).

  The matrix elements are grouped such that the first 8 elements (16 in s16 format) hold the 16-bit integer elements, and the next 8 elements (16 in s16 format) hold the 16-bit fractional elements. The Mt_t x type is declared as a long [4][4] matrix.

To declare a static unit matrix, the code would look as follows:

#include "gbi.h"
static Mtx ident =
{
/* integer portion: */
0x00010000, 0x00000000,     |1000|
0x00000001, 0x00000000,     |0100|
0x00000000, 0x00010000, --> |0010|     
0x00000000, 0x00000001,     |0001|     |1.00.00.00.0|
                                    -->|0.01.00.00.0|
/* fractional portion: */   |0000|     |0.00.01.00.0|
0x00000000, 0x00000000,     |0000|     |0.00.00.01.0|
0x00000000, 0x00000000,     |0000|
0x00000000, 0x00000000, --> |0000|
0x00000000, 0x00000000,     |0000|
};

A matrix with the translation elements (10.5, 20.5, 30.5) would look as follows.

mat.m[1][2] = (10 << 16) | (20);          | 1.0 0.0 0.00.0|
mat.m[1][3] = (30 << 16) | (1);      ---> | 0.0 1.0 0.00.0|
mat.m[3][2] = (0x8000 << 16) | (0x8000);  | 0.0 0.0 1.00.0|
mat.m[3][3] = (0x8000 << 16) | (0);       |10.520.530.51.0|

Note
Matrix concatenation in the RSP geometry engine is performed using 32-bit integer calculations. A 32-bit x 32-bit calculation produces a 64-bit value, and only the middle 32 bits remain in the new matrix (see the figure below). Therefore, when matrices are concatenated, fixed-point numerical values will generate errors.

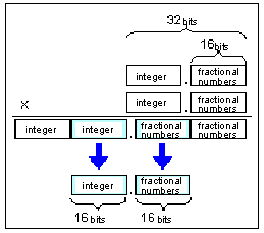
The middle 32 bits that remain in the new matrix

To maintain the highest precision, the absolute values of each component of the matrices must not differ significantly. Extreme scale and translation arguments will reduce the transformation precision. Since rotation matrix and projection matrix operations require very small fractional numbers, some of these may be lost when multiplied by large integer values. Also, the least significant bit (LSB) of each matrix term is rounded off when matrices are concatenated. As a result, a 1/2 LSB error is generated in the matrix for each concatenation. To guarantee full precision, concatenate the matrices using floating-point operations in the CPU and only load that result in the RSP.

Comment
Each G_MTX_MODELVIEW matrix operation is accompanied by an implicit matrix multiplication, even when G_MTX_LOAD is explicitly specified. The matrix which results from combining the model view (M) matrix and projection (P) matrix is used when the vertices are to be transformed by only a single matrix during the transformation.

One way to optimize the process is to concatenate modeling matrices in the CPU, and concatenate viewing (V) matrices and projection matrices in the projection matrix stack. When this is done, the MxVP matrix concatenation is carried out each time the modeling matrix is loaded. There are also other simple ways of concatenating modeling matrices. For example, a matrix that concatenates a rotation matrix around one axis with a translation matrix can be obtained by simply entering the appropriate elements for the matrix components.

The Mtx structure is as follows:

typedef long  Mtx_t[4][4];
typedef union{
        Mtx_t           m;
        long long int   force_structure_alignment;
} Mtx;

See Also
gSPForceMatrix
gSPInsertMatrix
gSPPerspNormalize
gSPPopMatrix